Julia set

Julia set

This blog post is meant as background information about my Julia sets generator.

In general, the Julia set is a set of numbers and is complementary to the Fatou set. These two sets are named after the French mathematicians Gaston Julia and Pierre Fatou who are the fathers of complex dynamics. The Mandelbrot set is a set of complex numbers and is found by Adrien Douady and named after french mathematician Benoit Mandelbrot. Both sets are bounded by fractals.

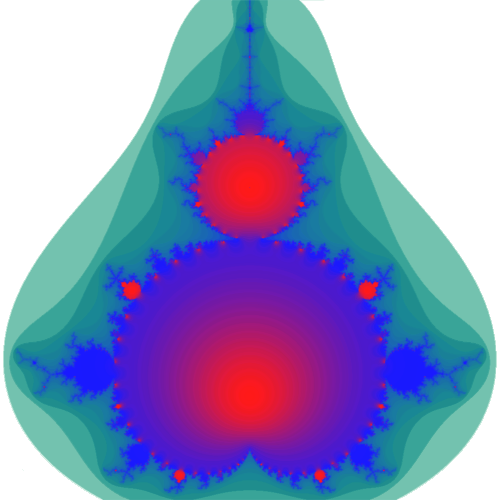Mandelbrot set

To obtain the Julia set, we need two variables, usually called $z$ and $c$. Both are complex numbers defined as $z=z_{real} + z_{imag}*i$ and $c=c_{real} + c_{imag}*i$. Different functions can be used to obtain a Julia set but most commonly used is the complex quadartic polynomial: $f(z) = z^2 + c$

We choose start values for all four numbers $c_{0,real}, c_{0,imag}, z_{0,real}, z_{0,imag}$ and then calculate $f(z)$ and use it as new $z$ value. This is repeated for a fixed number of iterations $n_{iter}$. If $|z|<2$ for $i< n_{iter}$, then the value belongs to the Julia set. This is repeated for all values $z_{real}$ and $z_{imag}$.

The Julia set can be visualized in a plane where for each $z_{real}$ and $z_{imag}$ the value $i/n_{iter}$ is plotted. Choosing different start values for $c_{real}$ and $c_{imag}$ renders different Julia sets. If we choose a fixed value for $z_0$, usually $z_0=0$, and plot the result for all values of $c$, we obtain the Mandelbrot set.

But why not just vary all four start values $c_{real}, c_{imag}, z_{real}, z_{imag}$? Well this is certainly possible but the result is a set of numbers in 4D hyperspace. That is quite hard to imagine and also hard to visualize.

To visualize (parts of) the 4D space, we choose a plane (2D) to actually show on the screen. To define it we need two 4D base vectors which span our plane plus a 4D position vector to fix the origin. For a position vector $(c_{real}, c_{imag}, z_{real}, z_{imag}) = (0,0,0,0)$ and base vectors $(1,0,0,0)$ and $(0,1,0,0)$ we obtain the typical Mandelbrot set, often called the “Apfelmännchen”. For different position vectors and base vectors $0,0,1,0$ and $0,0,0,1$ we obtain variations of the Julia set. But why limit ourselfs to these base vectors? We can choose any two base vectors and different origins, which renders many different and beautiful pictures of fractals. Try it out here with my Julia sets generator.

Helpful resources:

• Wikipedia Julia set
• Wikipedia Mandelbrot set
• https://www.larserikpersson.se/wp-content/themes/evol-one-theme/assets/images/chap9en/part4.html
• https://www.karlsims.com/julia.html